Le langage mathématique de la Beauté
L’explication du Nombre d’Or avait déjà été faite par Euclide, il y a plus de 2000 ans!
Le Nombre d’Or fut découvert par les Grecs de l’époque classique.
Il est même représenté par la lettre Phi φ (initiale du nom de Phidias, l’Architecte du Parthénon).
Sa première trace écrite remonte à -2000 av.J.C., dans un ouvrage qui compte parmi les livres les plus célèbres, les plus imprimés et les plus commentés de l’Histoire: les «Eléments de géométrie» d’Euclide. C’est le premier best-seller scientifique de l’histoire de l’humanité. On connaît très peu de choses sur Euclide.
Euclide d’Alexandrie naquit vers 325 av. JC et mourut en – 265 à Alexandrie. Il dirigeait en –300 le département mathématique au Temple des Muses de la ville d’Alexandrie, qui était le principal centre scientifique de toute la Méditerranée de l’époque. Il fut élevé à Athènes et de son vivant il était considéré comme l’un des grands talents de l’époque. La Bibliothèque d’Alexandrie contenait des manuscrits scientifiques les plus importants de l’époque. Les «Eléments de géométrie» ont été repris dans tous les manuels de géométrie de l’enseignement secondaire de tous les systèmes scolaires du monde.
Lorsqu’on décompose un objet en 2 parties inégales, on dit que la proportion est divine, ou dorée, si le rapport entre la grande partie et la petite est le même que celui entre le tout et la grande partie. Euclide exprime cela ainsi: «Le tout est à la partie ce que la partie est au Tout».
De nombreux objets de forme rectangulaire qui font notre quotidien ont été façonnés en fonction de la Divine Proportion. Ils nous paraissent particulièrement harmonieux.
On rencontre Phi φ dans la croissance des populations de lapins, décrite par Fibonacci au Moyen Age, dans celles du Parthénon d’Athènes, ou dans celles de nos cartes de crédit.
Que peuvent bien avoir en commun des phénomènes naturels aussi différents que l’agencement des graines d’une fleur de tournesol, l’élégante spirale dessinée par la coquille de certains mollusques (le Nautil notamment), les bras de la Voie Lactée, et la galaxie qui nous accueille?

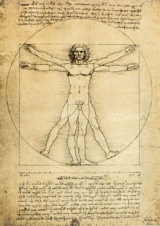
Quelle règle géométrique d’une inégalable harmonie se cache dans l’œuvre de grands artistes et architectes, de Vitruve à Le Corbusier en passant par Leonard da Vinci et Salvador Dali?
La réponse est un nombre simple, connu depuis l’Antiquité, qui apparaît dans toutes les représentations naturelles et artistiques: le Nombre d’Or, la Divine Proportion.
Il est à peine supérieur à 1, mais il est composé d’un nombre infini de décimales qui ne suivent aucune règle.
Il nous faut dessiner un rectangle dont la mesure du grand côté vaut celle du petit, multipliée par 1,618, donc un rectangle dont la proportion des deux côtés est le nombre d’or.
C’est un rectangle d’or.
Beaucoup d’artistes, peintres, architectes ont réalisé leurs œuvres sur base du Rectangle d’Or: la Grande Pyramide, des cathédrales françaises, le Parthénon… et même dans la Nature!
Le choix du Nombre d’Or comme étalon de mesure d’un modèle idéal de beauté n’est pas uniquement un caprice humain. Même la nature semble conférer à ce nombre un rôle spécial quand il s’agit de «choisir» une forme plutôt qu’une autre.
Pour la Reine des fleurs, la Rose, nous entrons aussi dans un univers où la proportion d’Or est l’organisatrice suprême: le règne végétal, avec un concept mathématique: la suite de Fibonacci.
La disposition des branches de certains arbres, le nombre de pétales de multiples fleurs, et la forme de leurs feuilles sont autant d’illustrations de la discipline de la Phyllotaxie qui étudie la disposition des feuilles sur une tige qui obéit à des règles géométriques.
On peut observer sur une plante quelconque que les feuilles ne poussent pas l’une sur l’autre, car elles se cacheraient l’une à l’autre la lumière du soleil dont elles ont besoin, la pluie et l’oxygène. Cela semble supposer une forme de conscience, non? Une analyse poussée de la disposition des feuilles sur la plante révèle un Patron, une organisation.
Le premier qui se rendit compte de ces propriétés, fut Léonard da Vinci. Il a découvert que les feuilles étaient disposées tout au long de la tige par groupes de 5, suivant des spirales, ce qui implique que l’angle de rotation soit en lien avec des multiples de 1/5.
Un peu plus tard, Kepler (astronome allemand du 17e siècle) étudia le mouvement des planètes avec Copernic et découvrit que les planètes tournent autour du soleil, contre la doctrine religieuse qui affirmait que la Terre était le centre de l’univers, observa que le pentagone était présent dans les fleurs et qu’elles avaient souvent cinq pétales. De même pour les fruits, dont les graines sont souvent disposées selon un pentagone étoilé, comme la pomme, coupée en deux.
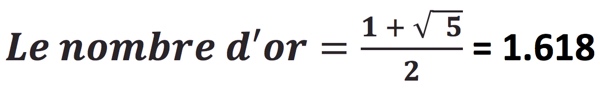
La suite de Fibonacci (1170-1250)
L’introduction du Nombre d’Or dans la Nature requiert l’introduction d’un nouveau concept: la suite de Fibonacci. Cette série numérique, décrite par le mathématicien italien du XIIIe siècle, démarre avec les chiffres 1 et 1, à partir desquels chaque nouveau terme est issu de la somme des 2 précédents:
1,1,2,3,5,8,13,21,34,55,89,144,233,377,610
Fibonacci, fils de marchand, né à Pise en 1170, s’est posé comme question: «Combien de couples de lapins aurons-nous à la fin de l’année si nous commençons avec un couple qui engendre chaque mois un autre couple qui procrée à son tour au bout de 2 mois de vie?»
Pour trouver la solution, il créa une table, une suite. On y voit que chaque terme s’obtient par la somme des 2 précédents et nous retrouvons la suite ci-dessus.
Des chercheurs du 19e siècle remarquèrent la présence des nombres de la suite de Fibonacci dans la pomme de pin. Au 2Oe siècle, des mathématiciens trouvèrent la même constante, quelle que soit la provenance des pommes de pin.
Quand on observe un tournesol, on aperçoit des spirales formées par les graines (les pépins) qui tournent dans les 2 sens d’une aiguille d’une montre. Les nombres de chacune d’entre elles sont aussi des termes consécutifs de la suite de Fibonacci.
Les branches d’un arbre ne naissent pas non plus entassées, mais en spirales. La taille d’un arbre varie tout au long de sa vie, mais son apparence extérieure, à savoir les proportions entre sa taille et la longueur de ses branches, de même que son aspect général, restent les mêmes.
Les fractales et le nombre d’Or (Benoît Mandelbrot – 1924-2010)
Le concept de fractale fit son apparition en 1975 grâce à Mandelbrot.
Une des caractéristiques des fractales est l’auto-similitude: la figure reste la même, et ce quelle que soit l’échelle. Que nous l’observions de près, de tout près, de loin, de très loin, de manière globale, ou dans le détail, l’image que nous verrons sera toujours la même.

Le chou romanesco est le meilleur exemple de fractale naturelle. Si nous coupons un morceau quelconque, sa forme est toujours la même que celle de l’ensemble.
Quand on compte les spirales qu’il forme dans les 2 sens de rotation, nous retrouvons le Nombre d’Or. Nous verrons aussi que ce sont les 2 termes consécutifs de la suite de Fibonacci: il y a 8 spirales vers la droite et 13 vers la gauche!
Nous constatons qu’un nombre ancien et vénérable, qui apparut dans les mathématiques il y a plus de 2000 ans, est toujours en parfaite connexion avec les connaissances mathématiques les plus avant-gardistes.
Le Nombre d’Or n’a rien d’une antiquité, il continue sa vie, plus vigoureux que jamais.
A l’Antenne de Lecher nous pouvons mesurer sur la L.O. 2.5, l’Energie Vitale qui est son expression.

0 commentaire